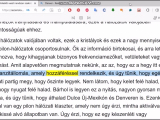
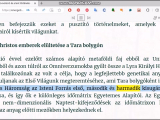
“…Egyszerre ott találta magát újra a Harvardon, a „Szimbolizmus a művészetben'' elnevezésű óráján, és a kedvenc számát írta föl éppen a táblára. 1,618 Langdon szembefordult a feszülten figyelő diáksereggel. — Ki tudná megmondani nekem, milyen szám ez? Egy hosszú lábú matek szakos emelte föl a kezét a hátsó sorban. — Ez a phi szám. — Fínek ejtette. — Kitűnő, Stettner — mondta Langdon. — Bemutatom önöknek a phit. — Nem tévesztendő össze a pivel — tette hozzá Stettner vigyorogva. — Ahogy mi, matematikusok mondjuk: a phi egy h-val különb a pinél. Langdon nevetett, de rajta kívül senki sem látszott érteni a viccet. Stettner lelombozódott. — Ez a szám a phi — folytatta Langdon. — Egy egész hatszáztizennyolc ezred, ami rendkívül fontos szám a művészetben. Tudja valaki, hogy miért? Megint Stettner igyekezett kitüntetni magát. — Mert olyan csinos? Mindenki nevetett. — Valójában — mondta Langdon — Stettner ismét igazat mondott. A phit tekintik ugyanis a legszebb számnak a Világegyetemben. A nevetés hirtelen abbamaradt, Stettner pedig kidüllesz-tette a mellét. Miközben Langdon betáplálta az írásvetítőt, elmagyarázta, hogy a phi szám a Fibonacci-sorozatból vezethető le — ez a haladvány nemcsak arról híres, hogy az egymást követő számok összege megegyezik az utánuk jövővel, hanem arról is, hogy az egymás melletti számok hányadosának az az elképesztő sajátossága, hogy mindig 1,618-at tesz ki*(A szomszédos Fibonacci-számok aránya (F_{n+1}/F_n\,) \phi\,-hez, az aranymetszésértékéhez tart (forrás: Wikipedia), tehát sosem éri el, de egyre pontosabban közelít hozzá). A phi szám látszólag misztikus matematikai eredete dacára, magyarázta Langdon, a phi legészbontóbb tulajdonsága mégis az, hogy a legelemibb építőkő szerepét játssza a természetben. A növények, állatok, de még az emberi lények térbeli sajátosságai is kísérteties pontossággal mutatják a phi az l-hez arányt. — A phi mindenütt jelenvaló a természetben — mondta Langdon, miközben lekapcsolta a világítást —, ami nem lehet véletlen, ezért tekintették az ókoriak a phit a Világegyetem teremtője által megszabott számnak. Az első tudósok isteni arányszámnak vagy aranymetszésnek nevezték. — Várjon — szólalt meg egy fiatal nő az első sorból. — Én biológia szakos vagyok, és még sohasem találkoztam az aranymetszéssel a természetben. — Nem? — vigyorgott Langdon. — Vizsgálta valaha a nőnemű és a hímnemű egyedek számarányát a méhek közösségében? — Természetesen. A nőnemű egyedek mindig többségben vannak. — Úgy van. És azt tudja-e, hogy ha a világ bármely kaptárában elosztja a nőnemű egyedek számát a hímnemű méhekével, akkor mindig ugyanazt a számot kapja? — Tényleg? — Bizony. A phit. A lány eltátotta a száját. — Az lehetetlen! — Pedig igaz — vágott vissza Langdon mosolyogva, miközben betolta egy tengeri kagyló képét a vetítőbe. — Felismerik? — Ez egy nautilusz — mondta a biológia szakos hallgató. — Egy puhatestű lábasfejű, ami gázt pumpál a háza kamráiba, és azzal szabályozza a merülését. — Helyes. És mit gondol, hogyan aránylik a kagylóhéj egyik spiráljának átmérője a másikéhoz? Mennyi az arányszám? A lány bizonytalan tekintettel méregette a nautilusz csigaházának spiráljait. Langdon bólintott. — Phi. Az aranymetszés. 1,618. A lány elképedten bámult. Langdon rátért a következő képre — egy kinagyított napraforgótányérra. — A napraforgómagok ellentétes csigavonalakban helyezkednek el. Kitalálják az arányszámot a két szomszédos sor átmérője között? — Phi? — kérdezték egyszerre. — Talált! Langdon egyre gyorsabban váltogatta a képeket a kivetítőben: fenyőtobozok, különböző levélelrendezésű növényi szárak, a rovartest részei, amelyek mind-mind az aranymetszés szabályának engedelmeskedtek. — Ez elképesztő! — kiáltott föl valaki. — Igen — mondta egy másik diák —, de mi köze van ennek a művészethez? — Örülök, hogy megkérdezte — válaszolta Langdon. Becsúsztatta a következő diát — egy halványsárga pergamenlap tűnt föl Leonardo da Vinci híres férfiaktjával, a Vitruvius-tanulmánnyal, amely Marcus Vitruviusról, a nagyszerű római építészről kapta a nevét, aki De Architectura című művében dicsőítette az aranymetszést. — Da Vincinél jobban senki nem értette az emberi test isteni felépítését. Holttesteket exhumáltatott azért, hogy megmérhesse az ember csontszerkezetének pontos arányait. Ő volt az első, aki kimutatta, hogy az emberi test a szó szoros értelmében építőkövekből áll, amelyek arányszáma mindig a phivel egyenlő. A teremben ülő hallgatók mind kételkedve néztek rá. — Nem hisznek nekem? — kérdezte Langdon. — Legközelebb vigyenek magukkal mérőszalagot, ha zuhanyoznak. Az osztály néhány futballistája felnyerített. — Nem csak a sportolók — reagált Langdon. — Mindannyian. Fiúk és lányok. Próbálják ki. Mérjék meg magukat a fejük búbjától a sarkukig. Az eredményt osszák el a köldöktől a sarkukig mért távolsággal. Találják ki, mi lesz a hányados! — Csak nem a phi? — tört ki hitetlenkedve az egyik focista. — De igen — felelte Langdon. — 1,618. Akarnak még egy példát? Mérjék meg a karjukat a vállukról az ujjuk hegyéig, azután osszák el a könyöküktől az ujjak hegyéig mért távolsággal. Megint a phi jön ki. Még egyet? Csípőtől a sarkukig osztva térdtől a sarokig. Megint csak a phi. Ugyanez a helyzet az ujjpercekkel, a lábujjakkal, a gerincoszlop arányaival. Phi, phi, phi. Barátaim, önök valamennyien két lábon járó emlékművei az aranymetszésnek. Langdon még a sötétben is érzékelte, hogy diákjai nem győznek álmélkodni. Jól ismert melegség járta át. Ezért szeretett tanítani. — Barátaim, láthatják, hogy a káosz mögött rend uralkodik a világban. Amikor az ókoriak felfedezték a phit, megvoltak győződve arról, hogy Isten építőkövére akadtak rá, amelyből a világot megalkotta, és leborultak a természet nagysága előtt. Nagyon is érthető, miért. A természetben Isten keze munkája nyilvánul meg, és mind a mai napig léteznek pogány, a Földanyát imádó vallások. Sokan ünnepeljük úgy a természetet, ahogy a régi pogányok tették anélkül, hogy tudnánk róla. A majális mint tavaszünnep tökéletes példa erre... a föld új életre ébred, hogy bőséget teremjen. Az aranymetszésben rejlő titokzatos varázslatot az idők kezdetén írták. Az ember pusztán csak játszadozik a természet törvényeivel, és mivel a művészet az ember arra tett kísérlete, hogy utánozza a Teremtő művének szépségét, elképzelhetik, hogy az aranymetszés milyen sok példájával találkozhatunk a művészetben e szemeszter során. A következő fél órában Langdon Michelangelo, Albrecht Dürer, Da Vinci és mások műveiről mutatott be képeket az osztálynak, bizonyítva az alkotók tudatos és szigorú ragaszkodását az aranymetszéshez kompozícióik elrendezésében. Igazolta a phi jelenlétét a görög Panthenón, az egyiptomi piramisok, sőt az Egyesült Nemzetek Szervezetének New York-i székháza építészeti arányaiban. Szervező struktúraként ott volt a phi Mozart szonátáiban, Beethoven V. szimfóniájában, Bartók, Debussy és Schubert zeneműveiben. Még Stradivari is a phi számot alkalmazta, mutatott rá Langdon, hogy kiszámítsa az f nyílás pontos elhelyezését híres hegedűin. — Befejezésül — mondta Langdon a táblához lépve — térjünk vissza a szimbólumokhoz. — Húzott öt, egymást metsző vonalat, amelyek egy ötágú csillagot adtak ki. — Itt láthatják az egyik legjelentősebb szimbólumot. Hivatalos elnevezése ötszög vagy pentagramma, ahogyan a régiek tisztelték. Számos kultúrában egyszerre tekintik isteni és mágikus jelképnek. Meg tudja valaki mondani, hogy vajon miért? A matek szakos Stettner emelte föl a kezét. — Mert ha felrajzolunk egy ötszöget, a vonalak automatikusan az aranymetszés szabályai szerint osztódnak részekre. Langdon elismerő pillantással jutalmazta a srácot. — Kitűnő válasz. Igen, a vonalszakaszok arányai az ötszögben mindig phivel egyenlők, ezért vált ez a szimbólum az aranymetszés legteljesebb kifejezőjévé. És ezért volt az ötágú csillag mindig is a szépség és a tökéletesség jelképe, amely az istennőre és a szent nőiségre utal.” " Dan Brown " ......................... Forrás:http://www.mosoly100.hu/content/phi-%E2%80%A6aranymets...